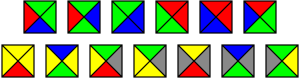
Suppose you want to cover the plane with square colored tiles. Tiles are chosen from a finite number of types and for each type you can have an unbounded number of them. The rule you want to follow is that tiles arranged side by side have abutting edges of the same color. Tiles cannot be rotated or reflected. Is it possible to cover the whole plane?
Below is an example of a set of tiles and the beginning of a tiling.
*The images above are from http://en.wikipedia.org/wiki/Wang_tile
You are not sure whether the entire plane can be tiled. Having written a number of Python programs and feeling confident about your problem solving abilities, you wonder if you should write a program that decides whether the plane can be tiled. If it can, the program should produce guidelines on how to do it.
There exists no Python program that takes as input a set of tiles and determines whether these tiles can be used to tile the entire plane. It has been mathematically proven that such a program cannot exist. The Wang Tile problem is what is called an undecidable problem.
For more information as well as historical background: