The Koch Snowflake is a type of fractal. A fractal is pattern that produces a picture which contains an infinite amount of copies of itself. It can be viewed as a drawing with a self-similar structure that is defined in terms of itself.
Here is an iterative way of drawing the Koch Snowflake:
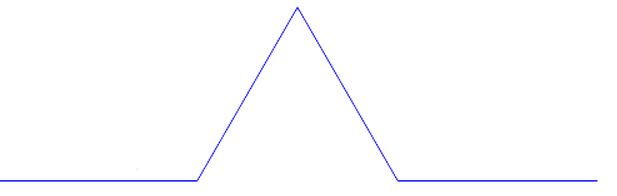
- Starting with a line segment, replace it with four new segments, each 1/3 the length of the original. The first and last segment aligns with the original line and the second and third segment form a unilateral triangle with the missing line. The result is shown below
- Repeat this process on all line segments of the resulting image.
- Repeat step 2 – the step replacing all line segments by four new segments – for as long as desired.
The resulting stages are shown at http://www.shodor.org/interactivate/activities/KochSnowflake/
What is a recursive definition of the Koch Snowflake?
Say, we want to produce the Koch Snowflake resulting from n iterations.
- When n=0, just draw a straight line.
- When n >0, recursively produce the Koch Snowflake resulting from n-1 iterations.
- Then, in the image resulting from step 2, replace each line segment by four new line segments (as shown above).
Writing a program that draws the Koch Snowflake using the iterative description has challenges. How can we print a line and then replace it? Programs drawing fractals, including the Koch Snowflake, always use recursion. We provide two recursive programs, one operating on the line and the other drawing a full snowflake.
If you cannot run the code in Canopy, the solution is here: https://support.enthought.com/entries/21793229-Using-Tkinter-Turtle-in-Canopy-s-IPython-panel
There exist many other recursive fractal programs. Students often like them as they draw attractive images and one can change them and experiment with them.
We provide code for two more. [Code Credit: http://interactivepython.org/XikcZ/courselib/static/pythonds/Recursion/graphical.html]
- Fractal Spiral (Fractals_Spiral.py)
- Use Python Turtle to draw a spiral recursively.
- Base case: when the length of the line we want to draw is reduced to the defined base or less.
- If the length of the line is longer than the base we defined, the turtle goes forward by lineLen units and then turn right 90 degrees.
- The recursive step is when we call drawSpiral again with a reduced length.
- Fractal Tree (Fractals_Tree.py)
- Use Python Turtle to generate a fractal tree
- Base case: when the branchLen is 10 or less, we draw a 10-unit long line and move our turtle back.
- If the branchLen is greater than 10, draw the tree recursively and reduce the branchLen