Eight suitcases are lined up in a row. They look identical. Seven of them have exactly the same weight and one is lighter than the others. You are given a balance scale that can measure suitcases against each other. Can you identify the lighter suitcase using the scale only twice?
We number the eight suitcases so we can identify them as they are placed on the scale.
Make sure to try some ways to weigh groups of suitcases before reading on. Also, feel free to substitute oranges, gold bars, chocolate bars or any other object for the suitcases.
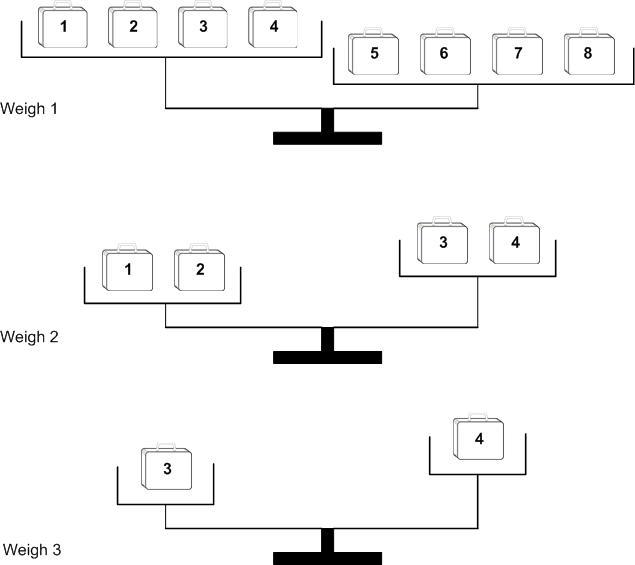
Here is how we can find the lighter suitcase by doing 3 weighs:
- Split the suitcases into 2 groups of 4 suitcases each. Put suitcases numbered 1, 2, 3, and 4 on the left side of the scale and 5, 6, 7, and 8 on the right side. Discard the four suitcases forming the heavier group on the scale.
- Take the remaining 4 suitcases and split into 2 groups of 2 suitcases each. Weigh and discard the two suitcases forming the heavier group on the scale.
- Do a final weigh on the two remaining suitcases to determine the light suitcase.
Illustration
Figure: Finding the light suitcase in three weighs
After the third weigh, we see that suitcase 4 is the lighter one.
Can we find the lighter suitcase using only 2 weighs? For some students it may seem impossible as they feel solving the problem with three weighs is already clever. Indeed, we can identify the lighter suitcase doing only two weighs!
Here is a hint: Don’t make the first weigh operation one that weighs 4 suitcases against 4 suitcases. What happens if we weigh fewer than 8 suitcases? Obviously the number of suitcases we weigh will always be even with equal numbers on each side.
Solution:
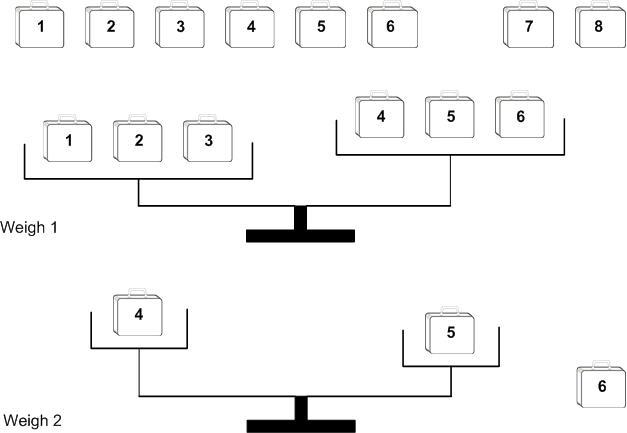
- Form two groups, one with 6 suitcases and one 2 suitcases. Put the group consisting of two suitcases to the side.
- Split the group consisting of 6 suitcases into two groups of 3 suitcases each and weigh them.
- Now proceed as follows to determine the second weigh operation
- If the suitcases in the weigh done in step 2 are of equal weight, discard the six suitcases. Perform one weigh on the two suitcases set aside in step 1. You have found the lighter suitcase!
- If the suitcases in the weigh done in step 2 are not of equal weight, they contain the lighter one. Discard the two suitcases set aside in step 1 (we know they have equal weight) and continue with the three suitcases containing the lighter one. Using the idea of setting one suitcase aside, we can determine the lighter suitcase in this group of three suitcases with a single weight. Done!
Illustration
Figure: Finding the light suitcase in two weighs
Both algorithms described contain if-then-else constructs that allow us to make the right decisions. Step 3 of the algorithm finding the lighter suitcase in two weighs contains a nested if-then-else construction that is worth pointing out.
Discussion topics:
- How do we find the lighter suitcase when we have more than 8 suitcases?
- Can we find the lighter suitcase in 2 weighs when we have 9 suitcases?
- How about 16 suitcases?
- How about a general strategy when we are given n suitcases? Assume first that n is a power of 2.
- What about the version when there are two lighter suitcases of equal weight?
- Produce a Scratch problem for the solution making 2 weighs.