While you may not have an immediate reason to organize data using a structure other than a list, the following briefly describes common data structures that students will encounter in a more advanced programming course.
Stacks
A stack is an ordered collection of elements where the addition of a new element and the removal of an existing element takes place at the same end, the top of the stack. A visual model of a stack are dishes in the cabinet, where the most recently cleaned dish placed in the cabinet will be put on the top and it is the first one removed from the cabinet the next time a plate is needed.
A stack is commonly referred to as a LIFO structure (Last In First Out). A stack can be implemented much like a list, but follows a specific model for how elements enter and exit. In a stack, elements are “pushed” on the list and “popped” off the list.
Queues
A queue is an ordered collection of elements where the new elements are added at one end, called the “rear,” and existing items are deleted from the other end, called the “front.” As an element enters the queue, it starts at the rear and makes its way toward the front. Eventually, it will be its turn to get deleted. A queue models a line to get a movie ticket, to get ones food in the cafeteria, to get on the bus, plus much more.
A queue can be implemented much like a list, but the queue follows a FIFO convention (First In First Out).
Dictionaries
A dictionary (sometimes known as a map) is a data structure where entries can be indexed by keys and not by integers (as done in lists and tuples). Dictionaries are a built-in data type in Python and are often convenient to use. Be aware that some students may use dictionaries when you want them to pursue a different implementation.
Assume you need to maintain the phone numbers of your students. For every student you have two entries: the name (a string) and a phone number (a seven-digit integer). The operations you want to perform are: (1) given a student name, find the phone number, and (2) given a phone number, determine the student(s) living at this phone number. A student can have only one phone number, but one phone number can be associated with more than one student.
The keys must be unique, while the values are allowed to be repeated. See introduction here: http://sthurlow.com/python/lesson06/
Example: Recording bird sightings
We want to record what birds we have seen how many times. The name of the bird is the key and the number of sightings is a value associated with the bird. A bird appears at most once in the structure. We want to update sightings and add birds.
birds1 = {'canada goose' : 3, 'northern fulmar' : 10}
print birds1 #returns {'northern fulmar': 10, 'canada goose': 3}
print birds1['northern fulmar' ] #returns 10
birds2 = {} # creates an empty dictionary
## Add new items
birds2['banded stilt'] = 2
birds2['black nunbird'] = 14
print birds2 # returns {'banded stilt': 2, 'black nunbird': 14}
## Delete an item
del birds2['banded stilt']
print birds2 #returns {'black nunbird': 14}
print birds1.items() #returns a list of birds1's (key, value) tuple pairs
print birds1.keys() #returns list of dictionary birds1's keys, which is ['northern fulmar', 'canada goose']
print birds1.values() #returns list of dictionary birds1's values, which is [10, 3]
Sets
A set is a type that does not allow duplicate data members and does not maintain any particular order. Sets are generally used to test for inclusion or exclusion of a particular member; another common operation is the union of two sets.
Graphs
A graph is an abstract data type that describes relationships between data points in a collection. Each data point is referred to as a node, and the connections between nodes are referred to as an edge. The edges can be directed or undirected depending on the application.
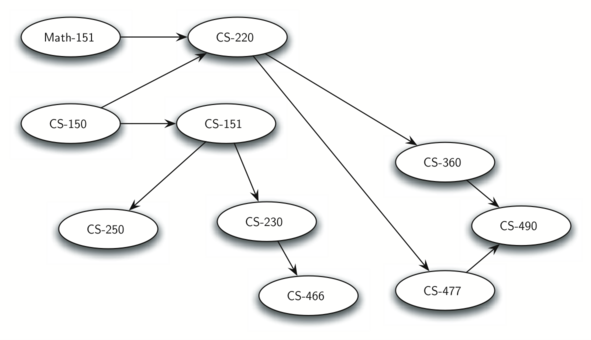
Example: Course Prerequisite Graph
A graph representing the prerequisites of courses
credit http://interactivepython.org/courselib/static/pythonds/Graphs/graphintro.html
Discussion Questions
- What courses have no prerequisites?
- What is the minimum number of semesters needed to take all courses?
- If a student can take at most three courses in a semester, what is the minimum number of semesters needed?
- Students should formulate additional questions. Statements need to be precise and unambiguous.
The prerequisite graph is a graph with directions on the edges. It contains no cycles. These types of graphs are called directed acyclic graphs (dags). They appear in many applications. Students should identify other applications that can be modeled by dags.
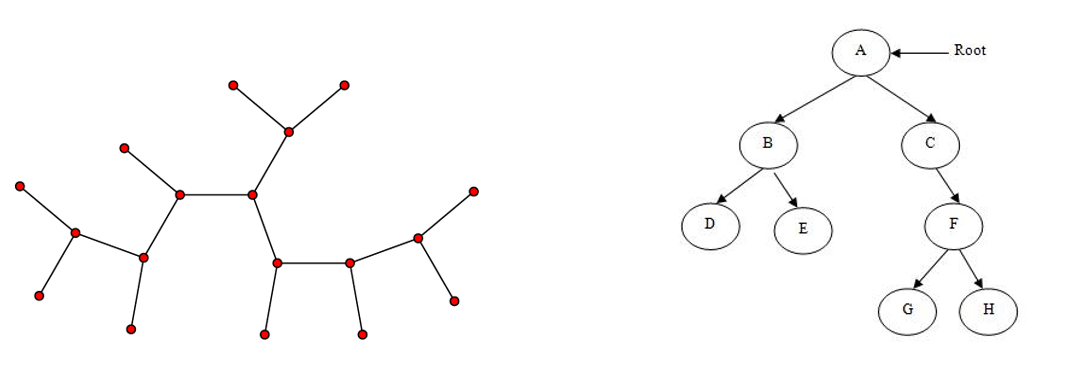
Trees
A tree is a special type of graph. If there are no directions on the edges, a tree is an undirected graph with no cycles and having a path between every pair of nodes. If there are directions on the edges, one node is typically identified as the root of the tree and all edges go either away from the root or point to the root. See examples of trees below.
Trees are a data structure modeling a special type of relationship. Trees are also used as a data structure to efficiently organize elements with keys. Binary search trees are an example of such a tree data structure.